Vector bundle connections. Connection form.

 Let \(E \rightarrow M\) a smooth vector bundle on a manifold \(M\). Let \(\Gamma(E)\) be the space of sections. A connection on \(E\) is an \(\mathbb{R}\)-linear map
\[
\nabla : \Gamma(E) \rightarrow \Gamma\left(E \otimes T^{*} M\right)
\]
satisfyng Leibniz rule
\[
\nabla(\sigma f)=(\nabla \sigma) f+\sigma \otimes d f
\]

This way, if \(X\) is a vector field one can define a notion of derivative of a section
\[
\nabla_{X} : \Gamma(E) \rightarrow \Gamma(E)
\]
by means of \(\nabla_{X} \sigma=(\nabla \sigma)(X)\).


If we think of sections like a generalization of functions or maps (I personally call them twisted functions) the connection is a device that let us derive this functions.
 

Connection form

Suppose we choose a particular local frame \(e=\{e_i\}\) (that is, we restrict to an open subset \(U\subseteq M\)). If we apply the connection to every \(e_i\) we obtain
\[
\nabla(e_i)=\sum_j e_i \otimes \omega_i^j
\]

The square matrix \(\omega=(\omega_i^j)\) of 1-forms is called the connection form. If our vector bundle is the tangent bundle, the connection form is not other thing that the usual Christoffel symbols!
 

Given a particular local section of \(E\), say
\[
\sigma= \sum_i \sigma_i e_i
\]
we have
\[
\nabla(\sigma)=\nabla(\sum_i \sigma_i e_i)=\sum_i e_i\otimes d\sigma_i+\sum_{ij}\sigma_i e_j\otimes \omega_i^j
\]
and renaming \(i\) and \(j\) in the second sum
\[
\nabla(\sigma)=\sum_i e_i\otimes\left( d \sigma_i+\sum_j \sigma_j \omega_j^i\right)
\]

So if we call \(\widetilde{\sigma}\) and \(\widetilde{\nabla(\sigma)}\) to the column vector of components of \(\sigma\) and \(\nabla(\sigma)\) respectively we have
\[
\widetilde{\nabla(\sigma)}=(d+\omega)\widetilde{\sigma}
\]
where \(d\) is the differential and \(\omega\) is a matrix of 1-forms.

Observe that an arbitrary matrix of 1-forms is a priori enough to define locally a connection.


If we choose a different frame \(e'=\{e'_i\}\) in \(U\), being
\[
e'=e g
\]
with \(g\) a matrix of smooth functions, it can be show that the new connection form will be
\[
\omega'=g^{-1} dg+g^{-1} \omega g
\]

This let us define a global connection form as a collection of matrices of 1-forms defined in an open covering of \(M\) satisfying certain compatibility condition in the overlaps.


Horizontal subspaces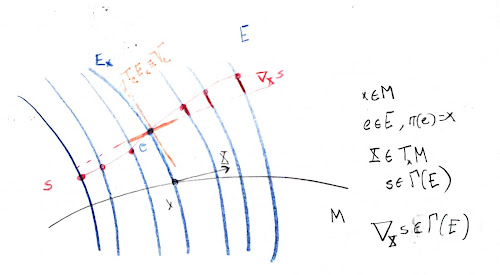



Consider now the space \(TE\).
For every \(e\in E\), with \(\pi(e)=x\in M\), we have a natural linear space \(T_e E_x\) that is called the vertical space. The union in \(e\in E\) gives us a subbundle \(V\subseteq TE\) called the vertical bundle.

At a first glance, there is no natural choice for an horizontal bundle, but \(\nabla\) determines one. We will define
\[
H_e:=ds_x (T_x M)
\]
where \(s\) is a section such that \(s(x)=e\) and \(\nabla_X s=0\) for every \(X\in T_x M\).

The idea of an horizontal subbundle gives rise to Ehresman connections.


In the next entry we are going to apply these ideas to a very simple model to get a deep understanding of them.


Comments

Post a Comment

Popular posts from this blog

About the definition of angle, from Geometric Algebra

Image
In GA, bivectors represent  2-dimensional directions. Any simple bivector can be written as \[ \theta e_1e_2 \] with \(\theta \in \mathbb{R}\) and \(\{e_i\}\) unitary and orthogonal vectors. The unitary vectors specify the 2- direction itself, and \(\theta\) is the size (analogous to the length of a vector, that is a 1-dimensional direction). Given two vectors \(a\) and \(b\) (that we take to be unitary, wlog) we say that the simple bivector \(\theta e_1e_2\) is the angle formed by them if \[ ab=e^{\theta e_1 e_2} \] where we take as a definition \[ e^A=1+A+A^2 /2+\cdots=\lim_N (1+\frac{A}{N})^N \] Real analysis let us assure that this expression is well defined when \(A\) is a 2-blade. In fact, since \(e_1e_2e_1e_2=-1\), we can write \[ e^{\theta e_1 e_2}=cos(\theta)+e_1 e_2sin(\theta) \] where \(cos\) and \(sin\) are defined by their power series. Oserve that \(b=a e^{\theta e_1 e_2}\) and then \[ b=a(cos(\theta)+e_1 e_2sin(\theta))=a\cdot cos(\theta)+ ae_1e_2 \cdot sin(\theta) \]
Read more

Spherical, hyperbolic and parabolic geometry

Image
Let's consider the space \(\mathbb{M}^4\), that is, the manifold \(\mathbb{R}^4\) with coordinates \((x,y,z,t)\) but with the pseudo-Riemannian metric given in each tangent space by \[ ds^2=dx^2+dy^2+dz^2-dt^2. \] This metric is left invariant by the group \(O(3,1)\) when acting on \(\mathbb{M}^4\). It also leaves invariant the cone \[ t^2-x^2-y^2-z^2=0 \] so is logical that we pay attention to it. Now, following TRTR from Penrose page 423, we can consider the family of hyperplanes inside \(\mathbb{M}^4\) given by \[ z+t+\lambda(t-z)=2 \] intersecting our cone in different 2-dimensional submanifolds \(P_{\lambda}\) of \(\mathbb{M}^4\). Here we have a picture from that book, where we consider only \((x,z,t)\) for purposes of drawability. If we analyse the case \(\lambda=0\), we observe that we obtain the submanifold \(P_0\), \(E\) in the picture with a shape of a parabola, given by the embedding \begin{align*}   \phi \colon \mathbb{R}^2 &\longrightarrow \mathbb{M}^4\\   (u_1,u_2
Read more

General covariance and contravariance (new version)

Image
Suppose that a group \(G\) acts transitively on a space \(X\). A transformation \(T\in G\) can be thought of indistinctly as either "moving" the objects in \(X\) or as a change of "point of view" in the following way: Suppose we have a comfortable, mathematically speaking, space with a distinguished point, \((S,s_0)\). We are going to think of \((\mathbb Z,0)\), for easy. Suppose also a bijection \(b_1:S\to X\) (in the line of reasoning of the notes homogeneous space#Intuitive approach and basis and change of basis ). It is better to think in terms of \(b_1^{-1}\). That is, for every \(x\in X\) we have a kind of "coordinates" \(s\) for \(x\), given by \(s=b_1^{-1}(x)\in S\). Think, for example, of a vector space \(V\) and the isomorphism \(b_1:\mathbb R^2 \to V\) (fixing a basis in \(V\)). We can think of this as our initial point of view , and we can imagine as if we were located at \(x_0=b_1(0)\in X\) with some devices to take measurements that let u
Read more