Cinf-structures to integrate involutive distributions

My collaborators and I have recently published two papers (this one and this other) in which  we develop a method to obtain the integral manifolds of involutive distributions. Exploring the integral manifolds of involutive distributions contributes to a broader understanding within differential geometry, an area with ties to many other mathematical branches. Furthermore, the study of these distributions and manifolds holds relevance in physics, especially within classical mechanics and field theory. A deeper grasp of these mathematical constructs can be beneficial for ongoing research in both mathematics and physics.

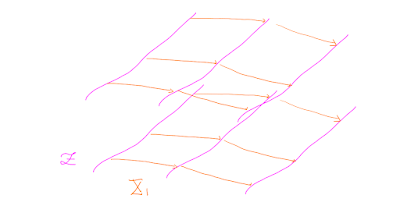
 Given a distribution, for example \(\mathcal{Z}=\{Z_1,Z_2\}\) in \(\mathbb R^n\), the idea of our work is to complete it with a sequence of \(n-2\) vector fields \(Y_1, Y_2,Y_3,\ldots\) in such a way that

- \(Y_1\) is a \(\mathcal{C}^{\infty}\)-symmetry of \(\mathcal{Z}\).
- \(Y_2\) is a \(\mathcal{C}^{\infty}\)-symmetry of \(\mathcal{Z}\oplus \{X_1\}\).
- \(Y_3\) is a \(\mathcal{C}^{\infty}\)-symmetry of \(\mathcal{Z}\oplus \{X_1,X_2\}\),
- and so on. 

The sequence is called a \(\mathcal{C}^{\infty}\)-structure for \(\mathcal{Z}\).

But, what is a \(\mathcal{C}^{\infty}\)-symmetry? Certainly, it is not a symmetry of distribution, but retains some of its characteristics. It is known that the flow of a symmetry of distributions, let's call it \(X_1\), carry integral manifolds of \(\mathcal{Z}\) into integral manifolds. 

 

(Here the integral manifolds of \(\mathcal{Z}\) are represented as curves, but represent higher dimensional manifolds.)

Well, a \(\mathcal{C}^{\infty}\)-symmetry doesn't do this, but at least its flow strings together an entire family of integral manifolds.


The following \(\mathcal{C}^{\infty}\)-symmetry in the sequence of a \(\mathcal{C}^{\infty}\)-structure would look like this:

where \(X_2\) would be a symmetry.

Here we proved, as a theoretical curiosity, that every \(\mathcal{C}^{\infty}\)-symmetry can be "corrected" to an autentic symmetry, but the process is by no means straightforward, and is not necessary for our method to work.

More specifically, a \(\mathcal{C}^{\infty}\)-symmetry of a distribution \(\mathcal{Z}\) is a vector field \(Y\) such that \(\mathcal{Z}\oplus \{Y\}\) is involutive. I.e., instead of the condition \([Y,\mathcal{Z}] \in \mathcal{Z}\), which characterizes symmetries, we now have 

\[[Y,\mathcal{Z}] \in \mathcal{Z}\oplus\{Y\}.\]

If the sequence of vector fields \(Y_1, Y_2,\ldots\) were made of proper symmetries instead of \(\mathcal{C}^{\infty}\)-symmetries, then we would have the important notion of solvable structure instead of a \(\mathcal{C}^{\infty}\)-structure. The key advantage of \(\mathcal{C}^{\infty}\)-structures is that \(\mathcal{C}^{\infty}\)-symmetries are easier to find than symmetries, and even if the process to obtain the integral manifolds of \(\mathcal{Z}\) have more obstacles than with solvable structures, in many cases it reaches a successful conclusion.

Let's show the method with a trivial example. Consider the distribution in \(\mathbb R^4\) given by the vector fields

\[
\begin{array}{rl}
    Z_1=&x_4 \partial_{x_1}+(x_2-x_3 x_4) \partial_{x_2}-x_3 \partial_{x_3}+x_4 \partial_{x_4},\\
    Z_2=&\partial_{x_1}+x_3 \partial_{x_2}+\partial_{x_4},
\end{array}
\]
which is involutive since \( [Z_1,Z_2]=-Z_2 \).

It can be easily checked that the vector fields
\[
\begin{array}{rl}
    Y_1=&x_4 \partial_{x_2}+\partial_{x_3}\\
    Y_2=&\partial_{x_4}
\end{array}
\]
constitute a \(\mathcal{C}^{\infty}\)-structure for \( \mathcal{Z} \), since
\[
\begin{array}{rl}
    [Y_1,Z_1]=&-Y_1,\\
    [Y_1,Z_2]=&0.\\
\end{array}
\]

Observe that we don't worry about the last vector field in a \(\mathcal{C}^{\infty}\)-structure, since any vector field linearly independent (pointwise) satisfies the condition.


We construct the following 1-forms:
\[
\begin{array}{rl}
    \omega_1=& \det(Z_1,Z_2,-,Y_2)=\\
                   =&-x^3 dx_1+x_3 dx_2+(x_2-2x_3 x_4)dx_3,\\
    \omega_2=& \det(Z_1,Z_2,Y_1,-)=\\
                  =&(x_2-x_3 x_4)dx_1-(x_2-x_3 x_4) dx_4.
\end{array}
\]
Then, since the distribution determined by \(\{Z_1,Z_2,Y_1\}\) is involutive, the 1-form \(\omega_2\) is Frobenius integrable, so we solve the completely integrable Pfaffian equation
\[
\omega_2\equiv 0,
\]
\[
(x_2-x_3 x_4)(-dx_1+ dx_4)\equiv 0,
\]
obtaining \( I_2(x_1,x_2,x_3,x_4)=-x_1+x_4 \). 

The submanifolds
\[
\Sigma_{(C_2)}=\{x\in \mathbb{R}^4:-x_1+x_4=C_2\}
\]
contains the integral manifolds of \(\mathcal{Z}\) so we restrict to them to continue our search. They are parametrized by
\[
\begin{array}{rccc}
\iota_2:& N_1 & \to & \mathbb{R}^4\\
        &(x_1,x_2,x_3) & \mapsto &(x_1,x_2,x_3,C_2+x_1)
\end{array}
\]
being \( N_1=\mathbb{R}^3 \). By pulling back with \( \iota_2 \) we obtain the 1-forms \( \langle \omega_1|_{\Sigma_{(C_2)}},\omega_2|_{\Sigma_{(C_2)}} \rangle \) defined on \( \Sigma_{(C_2)} \). We have that
\[
\omega_2|_{\Sigma_{(C_2)}}=0
\]
and
\[
\omega_1|_{\Sigma_{(C_2)}}=\iota_2^*(\omega_1)=-x_3^2 dx_1+x_3dx_2-(2 x_3C_2+2x_3x_1-x_2)dx_3.
\]

The Pfaffian equation \( \omega_1|_{\Sigma_{(C_2)}} \equiv 0 \) is also completely integrable, and a solution is given by
\[
I_1(x_1,x_2,x_3;C_2)=C2x_3^2+x_1 x_3^2-x_2 x_3.
\]

The submanifolds
\[
\Sigma_{(C_1,C_2)}=\{x\in N_1:I_1(x_1,x_2,x_3;C_2)=C_1\}
\]
are indeed the integral submanifold we are looking for. They are parametrized by
\[
\begin{array}{rccc}
\iota_1:& N_0 & \to & N_1\\
   & (x_1,x_2)& \mapsto & \left(x_1,x_2,\frac{x_2+\sqrt{4C_1C_2+4C_1 x_1+x_2^2}}{2 (C_2+x_1)} \right)
\end{array}
\]
being now the domain \( N_0 \) an open set of \( \mathbb{R}^2 \) which depends on \( C_1 \) and \( C_2 \) in such a way that \( \iota_1 \) is well defined.

This way, an explicit expression for the integral manifolds of \( \mathcal{Z} \) is
\[
\iota_2\circ \iota_1 : (x_1,x_2) \mapsto \left( x_1,x_2,\frac{x_2+\sqrt{4C_1C_2+4C_1 x_1+x_2^2}}{2 (C_2+x_1)}, C_2+x_1\right).
\]
The constants \( C_1, C_2 \) let us prescribe the point \( p\in \mathbb{R}^4 \) to be crossed by the integral manifold.
 

Comments

Post a Comment

Popular posts from this blog

About the definition of angle, from Geometric Algebra

Image
In GA, bivectors represent  2-dimensional directions. Any simple bivector can be written as \[ \theta e_1e_2 \] with \(\theta \in \mathbb{R}\) and \(\{e_i\}\) unitary and orthogonal vectors. The unitary vectors specify the 2- direction itself, and \(\theta\) is the size (analogous to the length of a vector, that is a 1-dimensional direction). Given two vectors \(a\) and \(b\) (that we take to be unitary, wlog) we say that the simple bivector \(\theta e_1e_2\) is the angle formed by them if \[ ab=e^{\theta e_1 e_2} \] where we take as a definition \[ e^A=1+A+A^2 /2+\cdots=\lim_N (1+\frac{A}{N})^N \] Real analysis let us assure that this expression is well defined when \(A\) is a 2-blade. In fact, since \(e_1e_2e_1e_2=-1\), we can write \[ e^{\theta e_1 e_2}=cos(\theta)+e_1 e_2sin(\theta) \] where \(cos\) and \(sin\) are defined by their power series. Oserve that \(b=a e^{\theta e_1 e_2}\) and then \[ b=a(cos(\theta)+e_1 e_2sin(\theta))=a\cdot cos(\theta)+ ae_1e_2 \cdot sin(\theta...
Read more

Spherical, hyperbolic and parabolic geometry

Image
Let's consider the space \(\mathbb{M}^4\), that is, the manifold \(\mathbb{R}^4\) with coordinates \((x,y,z,t)\) but with the pseudo-Riemannian metric given in each tangent space by \[ ds^2=dx^2+dy^2+dz^2-dt^2. \] This metric is left invariant by the group \(O(3,1)\) when acting on \(\mathbb{M}^4\). It also leaves invariant the cone \[ t^2-x^2-y^2-z^2=0 \] so is logical that we pay attention to it. Now, following TRTR from Penrose page 423, we can consider the family of hyperplanes inside \(\mathbb{M}^4\) given by \[ z+t+\lambda(t-z)=2 \] intersecting our cone in different 2-dimensional submanifolds \(P_{\lambda}\) of \(\mathbb{M}^4\). Here we have a picture from that book, where we consider only \((x,z,t)\) for purposes of drawability. If we analyse the case \(\lambda=0\), we observe that we obtain the submanifold \(P_0\), \(E\) in the picture with a shape of a parabola, given by the embedding \begin{align*}   \phi \colon \mathbb{R}^2 &\longrightarrow \mathbb{M}^4\\   (u_...
Read more

4-dimensional spheres, or haunting an ant

Image
In this post, we will try to explain a little bit what it feels like to live in a 4-dimensional world. First, we will see that we can enter the inside of a normal sphere without breaking the wall. And secondly, we will try to describe what we would feel if our world were not the classic 3D universe, known as \(\mathbb{R}^3\), but another 3-dimensional space called \(S^3\). But before we start, let's name things. The circles we all know have a more technical name for mathematicians: \(S^1\). On the other hand, a sphere (let's say, a ball) is called \(S^2\). This similarity in names is not accidental: since we were children, we intuitively knew that circles and spheres have something in common. In fact, they are "the same" except for the detail that circles are 1-dimensional (you can only move forward or backward), and spheres are 2-dimensional (if you lived in one, you could move forward-backward, but also left-right. Oops, actually, we live in one). Now let's ...
Read more