General covariance and contravariance (new version)

Suppose that a group \(G\) acts transitively on a space \(X\). A transformation \(T\in G\) can be thought of indistinctly as either "moving" the objects in \(X\) or as a change of "point of view" in the following way:

Suppose we have a comfortable, mathematically speaking, space with a distinguished point, \((S,s_0)\). We are going to think of \((\mathbb Z,0)\), for easy. Suppose also a bijection \(b_1:S\to X\) (in the line of reasoning of the notes homogeneous space#Intuitive approach and basis and change of basis). It is better to think in terms of \(b_1^{-1}\). That is, for every \(x\in X\) we have a kind of "coordinates" \(s\) for \(x\), given by \(s=b_1^{-1}(x)\in S\). Think, for example, of a vector space \(V\) and the isomorphism \(b_1:\mathbb R^2 \to V\) (fixing a basis in \(V\)). We can think of this as our initial point of view, and we can imagine as if we were located at \(x_0=b_1(0)\in X\) with some devices to take measurements that let us to create \(b_1\) .

An element of the group \(T\in G\) is a transformation, a movement, of \(X\) into itself.

The world description given by \(b_1\) let us define a map in \(\mathbb Z\) given by \(\tilde{T}_1=b_1^{-1}\circ T \circ b_1\equiv +6\)

\[ \begin{array}{cccc} \tilde{T}_1:& \mathbb Z &\to &\mathbb Z\\ &0&\mapsto&6\\ &3&\mapsto&9\\ &&...& \end{array} \]

Now, think that we ourselves have been shifted, so we can consider that we have a new point of view \(b_2\) of the world before the transformation. That is, the point of view 2 is how the red drawings is seen from the purple person. This new point of view satisfies \(b_2=T\circ b_1\), or \(b_2^{-1}=b_1^{-1}\circ T^{-1}\), if you want:

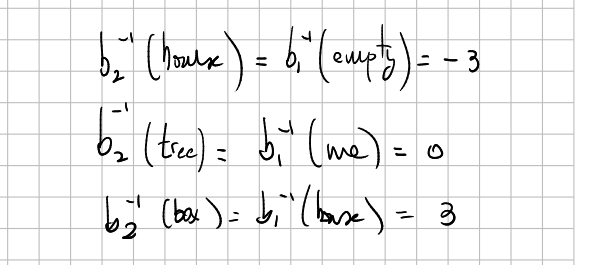
Also, \(b_2=b_1\circ \tilde{T}_1\).

The translation of point of view is a map \(f\) such that

\[ b_2^{-1}(\text{something})=f\circ b_1^{-1}(\text{something}) \]

Therefore \(f=\tilde{T}_1^{-1}\) since

\[ f=b_2^{-1}\circ b_1= \] \[ =b_1^{-1}\circ T^{-1}\circ b_1=\tilde{T}_1^{-1}\equiv -6 \]

So it turns out that to translate from point of view 2 to point of view 1 you have to substract 6 units, while the change itself has been produced by adding 6 units to the observer.It is impossible to distinguish whether the new description \(b_2^{-1}\) is caused by the world moving or by myself moving in the opposite direction.

Since the change of the "components" is opposite to the "transformation", it is said the the components are contravariant.

Very important example: covariance and contravariance in linear algebra.

Behavior of functions

Suppose a function \(h:X\to \mathbb R\) (in the pictures above think of the "height" of every object). The description given by \(b_1\) let us create a "more comfortable" function \(F_1:\mathbb Z\to \mathbb R\) given by \(F_1=h\circ b_1\), encoding the same data as in the diagram

\[ \begin{array}{ccc} X &\stackrel{h}{\longrightarrow} & \mathbb R\\ b_1\Big\uparrow & &\\ \mathbb Z&&\\ \end{array} \]

Consider a transformation \(T\) of \(X\) (think of a shift of +6, por example, in the picture above). What is the new comfortable description \(F_2\) of \(h\) with the new description \(b_2\) of \(X\)? Since \(b_2\) is the red drawings as seen by the purple person, it correspond to shift the graph by 6 units to the left:

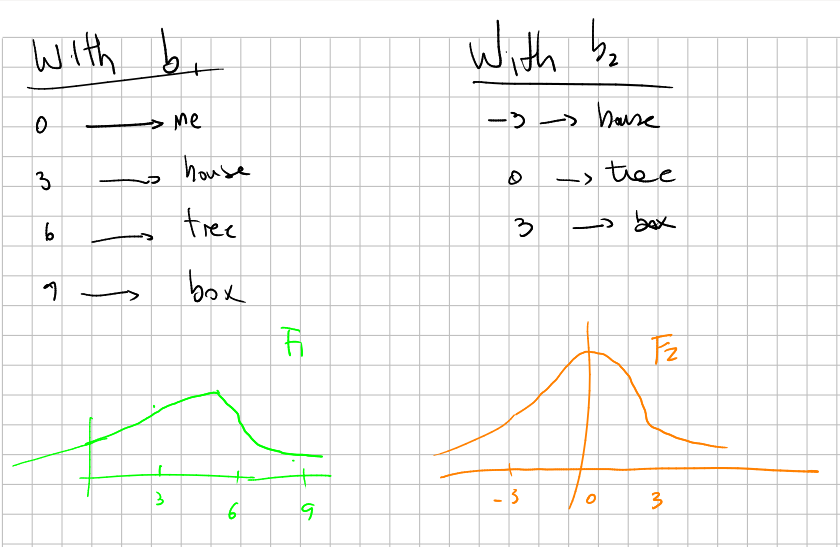
Analytically, the new description of \(X\) is \(b_2=T\circ b_1\),

\[ \begin{array}{ccc} \mathbb R&&\mathbb R\\ h\Big\uparrow & &h\Big\uparrow \\ X &\stackrel{T}{\longrightarrow} & X\\ b_1\Big\uparrow & &\\ \mathbb Z&&\\ \end{array} \]

so the new comfortable function is

\[ F_2=h\circ b_2=h\circ T \circ b_1=h\circ b_1 \circ b_1^{-1}\circ T \circ b_1= \]

and

\[ =F_1\circ \tilde{T}_1 \]

So if, for example, \(F_1(x)=x^2+1\) then \(F_2(x)=(x+6)^2+1\). Observe then that this correspond to the elemental fact in high school mathematics that to shift the graph of a function f(x) by \(a\) units you have to substitute \(f\) by \(f(x−a)\).

On the other hand, we may be interested in the implicit description of subsets of \(X\). How does the zero set of functions transform under \(T\)?

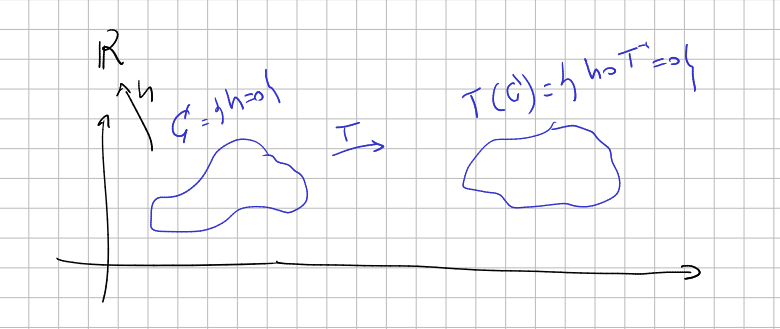
Consider \(C=\{h(x)=0\}\), the zero set of \(h\). The transformation \(T\) moves the set \(C\) to the set \(T (C)\). Since \(y\in T(C)\) if and only if there exists \(y'\in C\) such that \(y=T(y')\), with \(h(y')=0\). Then, \(h(T^{-1}(y))=0\), and therefore

\[ T(C)=\{x\in X: (h\circ T^{-1})(x)=0\} \]

i.e. the transformed function \(h\circ T^{-1}\) is just the function such that its zero set is the transformed of the zero set of \(h\). If we had started with \(T^{-1}\) instead of \(T\) we have arrived at the conclusion that \(h\circ T\) is the function whose zeroes are the translated by \(T^{-1}\), and then the function \(F_2=h \circ b_2=(h\circ T) \circ b_1\) have an interpretation different than above: is the description, in the first point of view, of the implicit function of the translation of \(C\) by \(T^{-1}\).

Particular cases:

Comments

Post a Comment

Popular posts from this blog

About the definition of angle, from Geometric Algebra

Image
In GA, bivectors represent  2-dimensional directions. Any simple bivector can be written as \[ \theta e_1e_2 \] with \(\theta \in \mathbb{R}\) and \(\{e_i\}\) unitary and orthogonal vectors. The unitary vectors specify the 2- direction itself, and \(\theta\) is the size (analogous to the length of a vector, that is a 1-dimensional direction). Given two vectors \(a\) and \(b\) (that we take to be unitary, wlog) we say that the simple bivector \(\theta e_1e_2\) is the angle formed by them if \[ ab=e^{\theta e_1 e_2} \] where we take as a definition \[ e^A=1+A+A^2 /2+\cdots=\lim_N (1+\frac{A}{N})^N \] Real analysis let us assure that this expression is well defined when \(A\) is a 2-blade. In fact, since \(e_1e_2e_1e_2=-1\), we can write \[ e^{\theta e_1 e_2}=cos(\theta)+e_1 e_2sin(\theta) \] where \(cos\) and \(sin\) are defined by their power series. Oserve that \(b=a e^{\theta e_1 e_2}\) and then \[ b=a(cos(\theta)+e_1 e_2sin(\theta))=a\cdot cos(\theta)+ ae_1e_2 \cdot sin(\theta...
Read more

Spherical, hyperbolic and parabolic geometry

Image
Let's consider the space \(\mathbb{M}^4\), that is, the manifold \(\mathbb{R}^4\) with coordinates \((x,y,z,t)\) but with the pseudo-Riemannian metric given in each tangent space by \[ ds^2=dx^2+dy^2+dz^2-dt^2. \] This metric is left invariant by the group \(O(3,1)\) when acting on \(\mathbb{M}^4\). It also leaves invariant the cone \[ t^2-x^2-y^2-z^2=0 \] so is logical that we pay attention to it. Now, following TRTR from Penrose page 423, we can consider the family of hyperplanes inside \(\mathbb{M}^4\) given by \[ z+t+\lambda(t-z)=2 \] intersecting our cone in different 2-dimensional submanifolds \(P_{\lambda}\) of \(\mathbb{M}^4\). Here we have a picture from that book, where we consider only \((x,z,t)\) for purposes of drawability. If we analyse the case \(\lambda=0\), we observe that we obtain the submanifold \(P_0\), \(E\) in the picture with a shape of a parabola, given by the embedding \begin{align*}   \phi \colon \mathbb{R}^2 &\longrightarrow \mathbb{M}^4\\   (u_...
Read more

4-dimensional spheres, or haunting an ant

Image
In this post, we will try to explain a little bit what it feels like to live in a 4-dimensional world. First, we will see that we can enter the inside of a normal sphere without breaking the wall. And secondly, we will try to describe what we would feel if our world were not the classic 3D universe, known as \(\mathbb{R}^3\), but another 3-dimensional space called \(S^3\). But before we start, let's name things. The circles we all know have a more technical name for mathematicians: \(S^1\). On the other hand, a sphere (let's say, a ball) is called \(S^2\). This similarity in names is not accidental: since we were children, we intuitively knew that circles and spheres have something in common. In fact, they are "the same" except for the detail that circles are 1-dimensional (you can only move forward or backward), and spheres are 2-dimensional (if you lived in one, you could move forward-backward, but also left-right. Oops, actually, we live in one). Now let's ...
Read more